Первый и Второй закон Кирхгофа для участка цепи

Когда возникает необходимость расчета или анализа электрической цепи, первое, что приходит в голову – применить законы Ома. Во многих ситуациях они позволяют рассчитать ток и напряжение на различных участках и элементах. Но не менее важно знать и уметь применять законы, названные именем немецкого физика Густава Кирхгофа (их иногда называют правилами) – они дают больше возможностей для анализа сложных и разветвленных цепей.

1 закон Кирхгофа

Перед тем, как начать рассматривать электротехнические законы, надо ввести несколько определений и терминов, которые будут применяться в дальнейшем:

• ветвь – участок цепи, по которой протекает один и тот же ток (последовательный участок);
• узел – точка цепи, в которой соединяются три и более ветви;
• контур – замкнутый путь в схеме, содержащий несколько ветвей и узлов.

Самая лаконичная формулировка первого правила (закона) Кирхгофа: сила тока в узле равна нулю.

Чтобы разобраться, что это означает, надо рассмотреть узел, объединяющий, например, 5 ветвей.

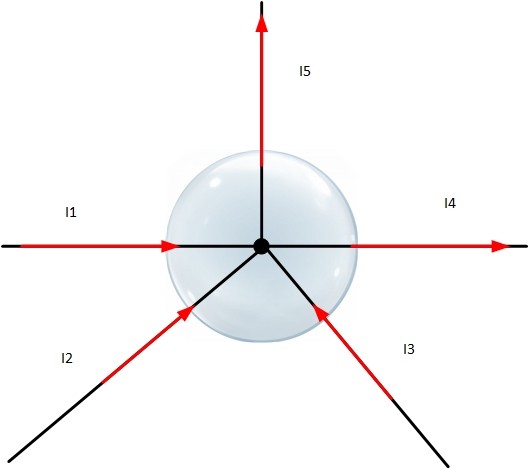
Пусть токи в ветвях 1,2 и 3 направлены в сторону узла, а в ветвях 4 и 5 в направлении от узла. Для наглядности можно представить сферу вокруг точки соединения, в которую втекают и вытекают токи. Тогда сумма втекающих токов I₁, I₂, I₃ по правилу Кирхгофа равна сумме вытекающих I₄, I₅: I₁+I₂+I₃=I₄+I₅ или I₁+I₂+I₃-I₄-I₅ =0. Следовательно, сила тока в узле равна нулю.

Здесь за положительное направление выбрано направление токов, втекающих в узел. Можно выбрать за базовое и противоположное направление, тогда все члены уравнения поменяют знак, а равенство останется верным.

Математически этот закон можно записать, как . Сформулировать его можно и по-другому:

Алгебраическая сумма токов в любом узле равна нулю.

Или совсем просто:

Сумма втекающих в узел токов равна сумме вытекающих.

2 закон Кирхгофа

Второе правило (закон) Кирхгофа гласит, что алгебраическая сумма ЭДС в замкнутом контуре будет равняться алгебраической сумме падений напряжений на всех резистивных элементах этой цепи. В виде уравнения это записывается, как . В этой формуле:

• ε – величина ЭДС, В;
• k – количество источников ЭДС в цепи;
• R – сопротивление элемента;
• I – ток через элемент;
• m – количество элементов в схеме.

Цепь, приведенная на схеме, содержит два источника ЭДС и три резистора. Так как резисторы соединены последовательно, то I=I₁=I₂=I₃.

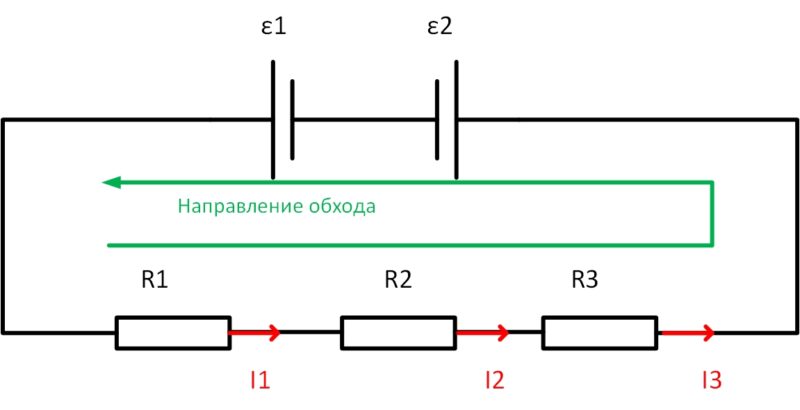
Направление обхода выбрано по часовой стрелке, поэтому можно записать выражение:

Направление обхода можно выбрать произвольно. При противоположном направлении обхода все члены уравнения сменят знаки на противоположные, но равенство останется верным.

Данная запись закона верна для цепей постоянного тока. Для цепей переменного уравнение примет вид , где:

• E – комплексная ЭДС;
• Z – полное (комплексное) сопротивление, учитывающее как резистивную, так и индуктивную, а также ёмкостную составляющие.

Читается это правило так:

Сумма амплитуд комплексных ЭДС равняется сумме комплексных падений напряжений на элементах схемы.

Правила Кирхгофа для разветвленных магнитных цепей

В теории магнитных цепей применяются понятия и физические величины, у которых хорошо прослеживается формальная аналогия с электрическими цепями:

• магнитное сопротивление можно сравнить с электрическим сопротивлением;
• магнитный поток является аналогом электрического тока;
• магнитное напряжение сравнивается с электрическим напряжением;
• магнитодвижущая сила является формальным аналогом электродвижущей силы.

Эти и другие аналогии можно применять, предполагая, что магнитное поле на каждом участке магнитопровода однородно.

Приняв эти формальные аналогии, к магнитным цепям можно применять правила и уравнения, аналогичные законам как Ома, так и Кирхгофа. Первое правило Кирхгофа в этом случае будет формулироваться: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.

В виде формулы этот закон можно записать, как  .

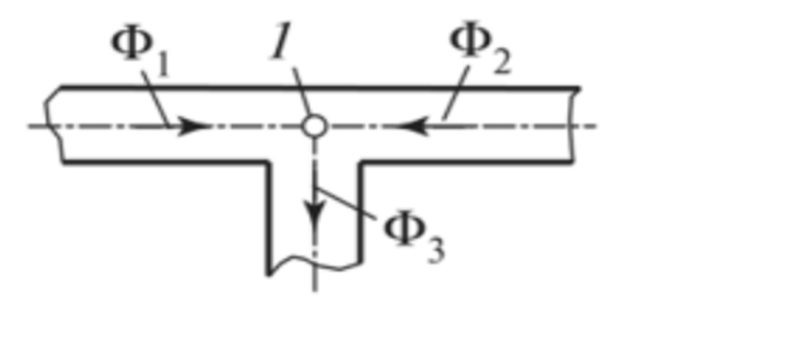
В качестве примера можно рассмотреть узел 1 в магнитной цепи, приведенной на рисунке в качестве примера. В него входят магнитные потоки Ф₁, Ф₂ и вытекает поток Ф₃. Приняв положительным направлением потоки, втекающие в узел, можно записать Ф₁+Ф₂-Ф₃=0.

Второе правило Кирхгофа можно сформулировать в виде:

алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль того же контура.

Формула для этого закона может быть записана в виде , где:

• U_m – падение магнитного напряжения на участке цепи Δl, на котором проекция напряженности магнитного поля равна Hl;
• I_nω_n – магнитодвижущая сила, создаваемая катушкой, равная произведению тока в катушке I на количество витков ω.

Известно, что падение магнитного напряжения равно Ф*R_m, где Ф – магнитный поток, а R_m – магнитное сопротивление участка цепи. Тогда второе правило можно записать в виде .

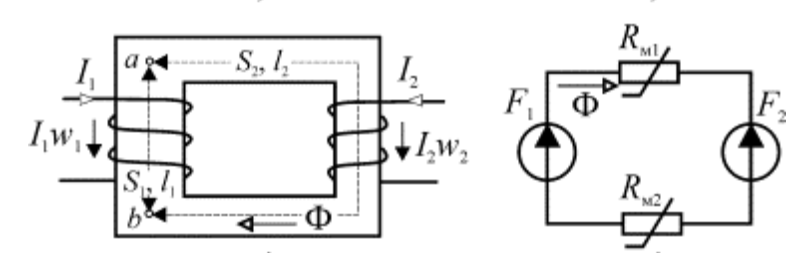
Иллюстрирует эту запись рисунок, на котором имеется сердечник с двумя обмотками с количеством витков ω₁ и ω₂, по которым идет, соответственно, ток I₁ и I₂. Направление МДС определяется направлением токов, которые направлены в разные стороны. Если взять направление тока в первой обмотке за положительное, то I₁ω₁— I₂ω₂= Ф*R₁+ Ф*R₁.

Понятия ветви, узла и контура для магнитной цепи также аналогичны подобным терминам для электрической цепи.

Применение законов для расчета

Для расчета параметров в большинстве случаев используются сразу оба правила. Общий порядок нахождения токов и напряжений таков:

1. Выбирается направление тока в цепи (можно произвольно).
2. Если в схеме n узлов, по первому правилу записывается n-1 уравнение.
3. Выбирается направление обхода контура (можно произвольно, если в схеме один источник ЭДС – удобнее в соответствии с этой ЭДС).
4. Если ЭДС и направление обхода совпадает, ЭДС в уравнение пишется с положительным знаком, если нет – с отрицательным.
5. Если ток в ветви и направление обхода совпадает, то падение напряжения на элементе ветви входит в уравнение положительным знаком, если нет, то с отрицательным.
6. Уравнения объединяются в систему, которую надо решить.
7. Если в результате токи получаются со знаком «минус», значит, их направления противоположны выбранному направлению обхода.

Расчет можно произвести на примере цепи, состоящей из трех резисторов и двух источников ЭДС. Их величины известны, требуется найти токи.

Элементы схемы образуют два контура, состоящие из:

• первый контур – резисторы R1, R3, источник ЭДС ε₁;
• второй контур – резисторы R2, R3, источник ЭДС ε₂.

Направления ЭДС в цепи показаны зелеными стрелками, выбранные направления токов в ветвях — красными. В узел А втекает ток I₃, вытекают I₂ и I1. Если выбрать положительным направление I₃, то можно записать:

I₃-I₂-I₁=0.

Выбранное направление обхода показано синими стрелками.

Так как резистор R3 принадлежит обоим контурам, направление обхода должно выбираться так, чтобы оно совпадало для этого резистора в двух контурах.

Применяя второе правило Кирхгофа, для каждого контура можно записать:

• I₁R₁+R₃I₃= ε₁;
• I₂R₂+R₃I₃= ε₂;

Добавляя первое равенство, можно получить систему из трех уравнений с тремя неизвестными:

• I₁R₁+R₃I₃= ε₁;
• I₂R₂+R₃I₃= ε₂;
• I₃-I₂-I₁=0

Решая эту систему, можно найти неизвестные параметры.

Освоив методы расчета простых цепей постоянного тока с помощью правил Кирхгофа, можно перейти к более сложному анализу цепей переменного тока, содержащих реактивности и комплексные величины.